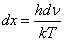Розв'язки задач

А тепер розглянемо розв'язання задач, які вміщені у попередній статті.

1. Згадаємо, що об'єм кулі (Землі) дорівнює

 

а об'єм циліндра (дроту) —  ,

де L — довжина циліндра, а d — його діаметр. Рівняючи ці об'єми, одержимо, що діаметр дроту становить

Підставляючи в одержану формулу значення відстаней від Землі до Сонця (1,5∙10⁸ км), до зорі α Центавра (1,3 пк=1,3∙3,1∙10¹³ км) і до Туманності Андромеди (7х10⁵°пк), знайдемо, що діаметри дротів дорівнюють 100 км, 200 м і 25 см відповідно. Задача справді нескладна, але результат дивний: дроти виявилися несподівано товстими. Справа тут у різній залежності об'єму від діаметра — у кубічній для кулі та квадратичній для циліндра, а підкореневий вираз у формулі для діаметра дроту залежить від куба радіуса Землі та першого степеня довжини дроту.

Ця задача наочно демонструє вплив показника степеня на залежність результату від певного параметра й водночас дозволяє порівняти значення трьох характерних відстаней у Всесвіті. її автор — відомий астрофізик-теоретик академік В. В. Соболєв.

 

2. Справжній мандрівник мусить уміти використовувати небесні явища для орієнтування в просторі та часі. Але припустімо, що наш мандрівник не практик, а теоретик. Тому він не знає зоряного неба, однак знає, який полюс планети є північним, а який південним. Визначити це можна в такий спосіб: з Північного полюса світу добове обертання планети виглядає як таке, що відбувається проти ходу годинникової стрілки. Тому обертання небесної сфери для спостерігача, який знаходиться у Північній півкулі планети, відбувається за годинниковою стрілкою, тобто зі сходу на захід. А в Південній півкулі це обертання, навпаки, виглядає як таке, що відбувається із заходу на схід. При цьому різниця в обертанні небесної сфери найбільш виразно виявляється саме в полярних зонах. Тому, спостерігаючи деякий час за переміщенням зір у їхньому добовому русі, мандрівник може визначити, на яку півкулю Землі він потрапив.

Звичайно, для Землі така ситуація з її полюсами склалася історично. Це правило визначення назв полюсів застосовується й щодо інших планет, точніше до тих, у яких осьове обертання відбувається в тому ж напрямку, що й рух за орбітою (таке обертання має назву прямого). Винятками з цього правила є Венера та Уран, які мають обернене осьове обертання. Для Венери це є наслідком припливного гальмування її обертання Сонцем і Землею. Що ж до Урана, то вісь його обертання, на відміну від решти планет, є близькою за напрямком до площини його орбіти. Це, мабуть, наслідок якоїсь катастрофічної події.

3. Насамперед з'ясуємо, про який саме місцевий час ідеться в умові задачі. Якщо, указуючи час події, не уточнюють, про який саме час ідеться, то мають на увазі місцевий середній сонячний час. Однак зрозуміло, що напрямок тіні визначається істинним сонячним часом, тобто положенням реального, а не середнього Сонця. Але найбільша різниця між істинним і середнім сонячним часом не перевищує 20 хв. Із цього випливає, що, нехтуючи різницю між цими двома способами вимірювання часу, ми зробимо похибку, яка не перевищує 5°. Тобто, висловлюючись мовою моряків, ми будемо шукати розв'язання нашої задачі з точністю до половини румба (румб — це кут, який дорівнює 1/32 повного кута, або приблизно 11°).

Дата, наведена в умові задачі, близька до моменту осіннього рівнодення, тобто схилення Сонця близьке до 0°. Інакше кажучи, вважатимемо, що Сонце знаходиться на небесному екваторі. Аналіз місцевого часу дозволяє визначити годинний кут Сонця. Оскільки початок сонячної доби збігається з нижньою кульмінацією Сонця, то о 15 годині його годинний кут і дорівнює 3^h, або 45° . А для того щоб визначити орієнтацію вікна, нам треба встановити азимут Сонця А в даний момент. Годинний кут відлічується вздовж небесного екватора, азимут — уздовж математичного горизонту. У свою чергу, те, як розташовані відносно один одного небесний екватор і математичний горизонт, залежить від широти місця, де ми знаходимося. Із відповідних визначень випливає, що кут між площинами цих великих кіл на небесній сфері доповнює широту місця спостереження до 90° . Тому на екваторі Землі небесний екватор розташований вертикально, але він завжди проходить через точки сходу та заходу. Отже, тінь від рами буде спрямована на схід, а вікно буде зорієнтоване на захід. Якщо ж ми наближатимемося до полюса, то кут між небесним екватором і горизонтом зменшуватиметься, наближаючись до нуля. Відповідно годинний кут та азимут зближуватимуться, тобто значення азимута буде наближатися до 45° . Орієнтація вікна наближатиметься до напрямку на південний захід. Зрозуміло, що на проміжних (помірних) широтах орієнтація вікна перебуватиме десь поміж заходом і південним заходом.

Вище було подано розв'язання задачі на якісному рівні, для якого достатньо було лише визначень відповідних основних ліній на небесній сфері та координат в горизонтальній та першій екваторіальній системах координат. Для кількісного ж розв'язання задачі потрібні вже дві основні формули сферичної тригонометрії — формули косинусів і синусів. Слід розглянути так званий паралактичний трикутник ZPS: «зеніт» — «полюс світу» — «світило» (у даному разі Сонце). Його сторони: ZР — доповнення широти місця спостереження до 90° , РS — доповнення схилення до 90° і ZS — зенітна відстань, кут при вершині Z доповнює азимут до 180° , а кут при вершині Р — це годинний кут. Тому формула косинусів (яка, до речі, може бути одержана як скалярний добуток відповідних одиничних векторів) з урахуванням того, що схилення дорівнює 0, дає:

де (φ — географічна широта. А формула синусів (що природно узагальнює формулу синусів плоскої тригонометрії) дасть значення синуса азимута:

Виконавши обчислення, наприклад для широти 50°, одержимо значення азимута Сонця А = 52,5° . Відразу ж зауважимо, що чверть, у якій лежить значення азимута, ми вже фактично визначили на попередньому етапі розв'язання задачі. У загальному ж випадку треба за відповідною формулою обчислити ще й косинус азимута, а потім, аналізуючи знаки синуса та косинуса азимута, визначити, у якій чверті знаходиться його значення.

Нарешті, відзначимо ще таке. По-перше, широта 50° - це широта Харкова. Але більшість обласних центрів України розташовані в широтній зоні 50° ±2° . Тому, ураховуючи сказане про точність нашого розв'язання, відповідь стосується й цих міст. Для одержання точнішої відповіді треба врахувати точніше значення їхньої широти та значення рівняння часу в день 22 вересня. По-друге, хоча розглядалася широта, близька до середньої між широтами екватора та полюса, значення азимута тіні ще мало відрізняється від 45°.

4.     Протони, викинуті під час хромосферного спалаху із Сонця, летять до Землі з постійною швидкістю. Щоб знайти цю швидкість, треба просто поділити відстань від Сонця до Землі на час, за який частинки досягають Землі і який дорівнює одній добі, тому

Тепер нескладно знайти кінетичну енергію протонів, згадавши, що їхня маса дорівнює 1,7∙10^-30 кг. Ця енергія дорівнює 2,5 10^-15 Дж. Для того щоб знайти значення цієї енергії в електрон-вольтах, треба поділити її на заряд електрона в кулонах (1,6 10^-19 Кл) , тому що електрон-вольт — це енергія, якої набуває електрон, пройшовши шлях в електричному полі з різницею потенціалів в 1 В. Одержимо остаточно, що середня енергія протонів сонячного вітру дорівнює приблизно 15 кеВ. Нагадаємо, що електрон-вольт — одиниця енергії, зручна для застосування в атомній фізиці та фізиці елементарних частинок, а в астрофізиці відповідні процеси відіграють важливу роль.

Звернемо увагу на те, що в розрахунках ми отримували не більш ніж дві значущі цифри. Це пов'язано з тим, що насправді різні протони одержують під час спалаху неоднакову енергію, надто під час різних спалахів. Тому йдеться лише про певне середнє, характерне значення енергії протонів і відповідно про середній час досягнення ними Землі. Це підкреслено в умові задачі виразом «приблизно за добу».

5.     Найбільш інформативним з астрономічного погляду є уривок із незакінченого вірша Пушкіна. Захід у поета розташований праворуч, значить, стояв ліричний герой обличчям на південь. Захід темно-червоний, тобто час доби — вечір, Сонце щойно зайшло. Місяць — ліворуч, навпроти Сонця. Значить, фаза Місяця близька до повні. Нарешті, Місяць — «близький». Це наслідок того, що світило знаходиться низько над горизонтом, коли воно здається більшим (а тому і ближчим), ніж завжди. Удаваний розмір Місяця в цьому випадку зумовлений тим, що він спостерігається на тлі віддалених земних об'єктів поблизу горизонту.

Крім того, Пушкін пише: «Надо мной в лазури ясной светит звездочка одна». Що це за світило? «Наді мною» — значить, воно знаходиться високо над горизонтом. «У лазурі ясній» — значить, на ще світлому небі, тобто це досить яскраве світило. Але це не можуть бути найяскравіші світила нашого неба Венера або Сиріус. Венера — внутрішня планета, вона не може розташовуватися далеко від Сонця, а Сиріус має від'ємне схилення й у наших широтах не піднімається високо. Найімовірніше, це одна з найяскравіших зір літнього неба а Ліри — Вега.

У наступних трьох уривках ідеться про колір Місяця. У Лєрмонтова він білий, у Єсеніна — золотий (жовтий), у Чехова — червоний. І кожний з них має рацію. Справа тут у різному впливі земної атмосфери на забарвлення світила, що спостерігається, залежно від його висоти. У разі розсіяння світла на частинках повітря (точніше кажучи, на теплових флуктуаціях густини повітря) кількість розсіяного світла обернено пропорційна четвертому степеню довжини світлової хвилі. Під час розсіяння світла пиловими частинками ця залежність не така сильна, але все ж таки ефективніше розсіюється більш короткохвильове світло. Якщо світило стоїть високо над горизонтом, то світло проходить крізь відносно невелику товщу атмосфери й колір світила практично не змінюється. Якщо ж висота світила невелика, то товща атмосфери, крізь яку проходить світло, значно збільшується (приблизно як косеканс висоти) і розсіянням видаляється значна частина світла, насамперед із коротшою довжиною хвилі, тобто спочатку слабнуть сині промені, потім жовті й так далі. Мабуть, Лєрмонтов описав своє враження від зимового Місяця, який стояв високо в небі, бо саме взимку Місяць у повні спостерігається високо над горизонтом, оскільки Сонце взимку опускається глибоко під горизонт. Єсенін бачив Місяць, розташований порівняно низько, а герої чехівського оповідання «Аптекарка» поба­чили Місяць біля самого горизонту (бо кущі були віддалені).

Слід віддати належне М. Лєрмонтову. Він звернув увагу на ще одну особливість Місяця, написавши, що Місяць у небі «точно блин». Цим порівнянням поет підкреслив, що Місяць має вигляд не об'ємного тіла, а плоского диска. Відбувається це не тільки тому, що зір людини не сприймає форм об'єму на великій відстані. Особливістю Місяця є те, що в повні яскравість деталей на його поверхні не залежить від їхнього положення на місячному диску: вона однакова й у центрі, і на краю Місяця. Звернув увагу на це ще Г. Галілей — перша людина, яка поглянула на Місяць і взагалі на небо в телескоп. Він правильно пов'язав це явище з великою шорсткістю місячної поверхні. Довів же цей факт шляхом відповідних вимірювань український астроном М. П. Барабашов. Якби поверхня Місяця була світлою та матовою, то яскравість її була б пропорційною косинусу падіння сонячних променів і краї місячного диска були б темнішими від його центральної частини, що створювало б ефект об'ємності Місяця.

Зауважимо, що ми вважали за можливе й навіть потрібне зберегти мову оригіналу у використаних уривках із художніх творів, бо їхніми авторами є найвидатніші майстри слова.

6. Час досягнення Південного полюса снарядом-супутником Землі визначається як половина періоду його обертання навколо Землі. Щоб знайти цей час, треба довжину півкола πR_З (R_з — радіус Землі) поділити на першу космічну швидкість:

Одержимо, що час

Зауважимо, що формулу для першої космічної швидко­сті нескладно отримати, якщо дорівняти прискорення віль­ного падіння, яке визначається згідно із законом всесвітнього тяжіння як  

доцентровому прискоренню 

Час руху снаряда в шахті визначити складніше. Річ у тому, що в кожний момент він притягується лише тією частиною маси Землі, яка міститься всередині сфери, що проходить через миттєве положення снаряда. Тому першу половину свого шляху снаряд проходить, рухаючись прискорено, але величина прискорення зменшується до нуля в центрі Землі. Закон цього зменшення залежить від змінення величини маси, яка притягує снаряд, а остання, у свою чергу, залежить від закону зміни густини Землі вздовж її радіуса. Але можна відповісти на питання задачі, якщо розглянути прості граничні випадки розподілу густини в планеті, поміж якими знаходиться цей розподіл для реальної Землі.

Випадок 1. Однорідна планета (модель Ньютона) — густина ρ не залежить від відстані до її центра. Тоді на відстані r від центра маса, що притягує снаряд, дорівнює

а прискорення снаряда дорівнює відповідно

Знак «-» указує на те, що радіус-вектор і вектор прискорення протилежно спрямовані. Але вираз для прискорення показує, що воно за величиною є пропорційним відстані до центра, тобто ми маємо тут справу з таким же законом для сили, як у випадку пружних коливань. Це значить, що півперіод коливання (час, який нам і треба визначити), можна знайти за аналогією до формули для півперіоду малих коливань маятника:

де L — довжина маятника, а g — прискорення вільного падіння на поверхні Землі. Прискорення ж маятника

де r — відхилення маятника від положення рівноваги в горизонтальному напрямку. Порівнюючи вирази для прискорень маятника та нашого снаряда, одержимо, що час руху останнього

Цікаво, що цей час збігається з часом руху супутника по півколу.

 Випадок 2. Уся маса планети зосереджена в її центрі (дуже мале важке ядро й дуже легка оболонка, модель Гюйгенса). У цьому разі потрібний час можна знайти двома шляхами. Перший — це інтегрувати від 0 до R_З рівняння прямолінійного руху з прискоренням 

 другий — розглянути прямолінійний рух снаряда від поверхні до центра Землі як рух за гранично стисненим еліпсом з ексцентриситетом, що дорівнює 1. Те ж стосується й руху снаряда від центра до Південного полюса. Тоді, за третім законом Кеплера, повний час руху снаряда дорівнюватиме періоду руху за еліпсом із великою піввіссю

та відрізнятиметься від випадків Т₁ і Т_2а множником 

.

 Тож ми отримаємо, що час

Час руху снаряда в реальній Землі задовольнятиме нерівність Т_2b<Т₂<Т_2а і буде меншим від часу руху снаряда-супутника за коловою орбітою.

Стан невагомості в снаряді, що рухається в шахті, звичайно, буде, бо вага — це реакція опори, а за будь-якого вільного руху ця реакція відсутня.

До Південного полюса снаряд у шахті прийде з нульовою швидкістю. У першому випадку це випливає з аналогії з маятником, а в загальному випадку — із симетрії задачі відносно центра Землі.

Корисно звернути увагу учнів на те, що прийом, застосований у цій задачі,— знаходження меж, у яких лежить шукана величина,— є досить типовим для фізики й астрономії.

7. На жаль, із новорічною вечерею при свічках в екіпажу орбітальної станції нічого не вийде. Для горіння свічки потрібен кисень, тому в повітрі, яке безпосередньо оточує полум'я свічки, його вміст швидко зменшиться. Але це ж полум'я нагріває повітря. Нагріте повітря розширюється, стає легшим і піднімається вгору. На його місце надходить холодніше повітря, збагачене киснем, що в цьому разі є найважливішим. І свічка продовжує горіти. Явище піднімання нагрітого повітря вгору зветься конвекцією. Вона виникає тоді, коли виштовхувальна сила Архімеда стає більшою від ваги нагрітого повітря. А на орбітальній станції в умовах невагомості конвекція не виникатиме, і свічка швидко згасне. Узагалі, відсутність конвекції в газі або рідині в невагомості — це суттєва особливість умов на борту космічного апарата.

8. Молярна маса — це маса атома чи молекули в атомних одиницях маси, практично в частках маси протона. Тому здається, що вона не може бути меншою від 1, бо такою вона є в найлегшого атома — атома Гідрогену. Але речовина Сонця нагріта до дуже високих температур — від 6000 К біля поверхні до 15 млн К у центрі. Тому вона вся (за винятком дуже тонкого поверхневого шару) повністю йонізована. Більшу частину речовини Сонця становить Гідроген (приблизно 70 % за масою). Під час йонізації Гідрогену одержуємо дві частинки — протон та електрон. Маса електрона дуже мала (у 2 тис. разів менша від маси протона). Тому молярна маса суміші протонів та електронів практично дорівнює 0,5. Решту, майже 30 % маси Сонця, становить Гелій, частка більш важких елементів не перевищує 2 %. Молярна маса Гелію дорівнює 4, але за повної його йонізації утворюється два електрони, тобто всього три частинки, тому молярна маса повністю йонізованого Гелію дорівнює 4/3. Як тепер знайти молярну масу суміші йонізованих Гідрогену та Гелію? Слід скористатися рівнянням стану ідеального газу:

Де р — тиск, R — універсальна газова стала, ρ — густина, а Т — температура. Однак такому ж рівнянню стану під­коряється не тільки суміш газів, але й кожний газ окремо, тобто маємо:

Але повний тиск створюється сумою тисків окремих газів, а їхні густини дорівнюють 0,7 і 0,3 від повної густини суміші. Складаючи праві частини останніх двох рівнянь із відповідними масами й дорівнюючи отриману суму правій частині попереднього рівняння, одержимо, що

Підставляючи значення молярних мас йонізованих Гідрогену та Гелію, одержимо, нарешті, значення молярної маси речовини Сонця, яке дорівнює приблизно 0,6.

Щоб знайти тепер повну кількість частинок, які утворюють Сонце, треба лише поділити його масу на добуток µm_p:

Тепер, за бажанням, можна оцінити повне число нуклонів у Всесвіті, згадавши, що в Галактиці приблизно 400 млрд зір, а в Метагалактиці — близько 1 млрд галактик. Матиме­мо таку оцінку за порядком величини: 

9. Яскравість не самосвітної, а відбивної поверхні (а саме такою є поверхня Місяця) пропорційна її освітленості та відбивній здатності. А освітленість від точкового (або сферично симетричного джерела, яким і є Сонце) змінюється обернено пропорційно квадрату відстані до нього, тому відношення середніх яскравостей дисків Місяця та Сонця

де А — відбивна здатність поверхні Місяця, R — радіус Сонця, r — середня відстань від Сонця до Місяця, яка дорівнює 1 а. о. Обчислення показують, що 

Перш ніж перейти до наступних задач, нагадаємо необхідні відомості про закони теплового випромінювання. Якщо електромагнітне випромінювання перебуває в термодинамічній рівновазі з речовиною, яка поглинає все випромінювання, що падає на неї (абсолютно чорне тіло), то інтенсивність випромінювання такою речовиною (кількість енергії, що її випромінює одиниця поверхні в одиничному тілесному куті та одиничному інтервалі довжин хвиль за одиницю часу) залежить тільки від температури поверхні та визначається законом (або функцією) Планка:

де h — стала Планка, с — швидкість світла, k — стала Больцмана (це множник переходу від температури до енергетичних одиниць), e=2,718 — основа натуральних логарифмів. Якщо підсумувати випромінювання на всіх довжинах хвиль (тобто проінтегрувати функцію Планка від 0 до нескінченності за λ), то одержимо повну кількість енергії, що випромінюється з одиниці поверхні в одиницю тілесного кута за одиницю часу, яка визначається законом Стефана-Больцмана:

де σ — стала Стефана — Больцмана, вона дорівнює:

Повна ж потужність випромінювання з одиничної площадки дорівнює πВ(Т).

У функції Планка є один максимум. Його положення та значення залежать від температури: чим вищою є температура, тим на коротшій хвилі буде розташований цей максимум ( — закон зміщення Віна, b=0,29см) і тим більше значення він матиме. Якщо температура поверхні настільки мала, що у видимому оком діапазоні спектра випромінюється дуже мало енергії, то поверхня буде справді здаватися чорною. Якщо ж максимум випромінювання потрапляє у видимий діапазон довжин хвиль, то поверхня буде яскравою, колір її визначатиметься тим, у яку частину спектра (синю, жовту і т. д.) потрапляє цей максимум.

У наступних задачах будемо вважати, що умови застосування вищенаведених законів виконуються.
 10. По-перше, з'ясуймо, що означають слова «у спекотнии місячний полудень». Місячна поверхня нагрівається тією часткою сонячного випромінювання, яку вона поглинає і яку сама потім випромінює згідно із законами теплового випромінювання. Для того щоб знайти енергію, що її поглинає одиниця поверхні Місяця, треба знати сонячну сталу Е (кількість енергії, що приходить до одиничної площадки, яка є перпендикулярною до напрямку на Сонце, за одиницю часу на середній відстані Землі та Місяця від Сонця, ). Тоді повна кількість сонячної енергії, що її перехоплює Місяць, дорівнює πR²∙E , де R — радіус Місяця, а випромінюється частка цієї енергії, яка дорівнює 1-А, де А — відбивна здатність місячної поверхні. З другого боку, повна кількість енергії, яка випромінюється згід­но із законом Стефана-Больцмана, дорівнює  . Зрівнюючи ці кількості енергії, знайдемо з одержаного рів­няння температуру поверхні. Матимемо, що температура  

Множник 2 у знаменнику підкореневого виразу з'являється тому, що площа півсфери Місяця, яка освітлюється Сонцем, удвічі більша від поперечного розрізу Місяця. Зауважимо, що температура, яку знаходять таким чином, має назву ефективної. Обчислення ефективної температури місячної поверхні, освітленої Сонцем, дає значення T=388 К. Справді спекотно — більш ніж +100 °С. Що ж відбудеться з температурою залитої білилами залізної поверхні? Її відбивна здатність є близькою до 1, і з одержаної формули видно, що температура поверхні знизиться. Нехай (для визначеності) відбивна здатність білил дорівнює 99 % . Тоді температура поверхні становитиме всього 123 К, або -150°С,— довго на ній встояти справді буде важкувато. Мають виникнути питання: чому йдеться саме про залізну поверхню й чому можна знехтувати її нагрівання від місячного ґрунту? Мала теплоємність заліза приведе до того, що поверхня швидко остигне, мала теплопровідність дуже пористого місячного ґрунту заважатиме передачі тепла від ґрунту до більш холодної залізної поверхні.

Нарешті, слід зауважити, що під час розв'язання цієї задачі ми не враховували ще такої обставини. Певна частина сонячного випромінювання (довгохвильовий «хвіст» його спектра) лежить в інфрачервоній частині, де відбивна здатність білил зменшується. Тому температура залізної поверхні, залитої білилами, буде насправді дещо вищою.

Стосовно доцільності побудови астрономічної обсерваторії на Місяці, то вона пов'язана насамперед із відсутністю на ньому атмосфери. Земна атмосфера взагалі пропускає випромінювання небесних тіл лише в оптичному діапазоні та певній частині радіодіапазону. В оптичному діапазоні вона спотворює спектральний склад випромінювання, а головне, обмежує роздільну здатність телескопів. Відсутність розсіяного атмосферою світла дозволяє вести спостереження на Місяці не тільки вночі, але й удень, а мала швидкість добового обертання Місяця спрощує проблему гідування під час спостережень.

11. Знайти сонячну сталу для Венери нескладно. Для цього треба сонячну сталу для Землі поділити на квадрат великої півосі орбіти Венери, виражену в астрономічних одиницях. Потім можна знайти ефективну температуру Венери за формулою попередньої задачі, для чого треба знати відбивну здатність Венери. її поверхня вкрита суцільним шаром хмар. Хмари досить світлі, можна прийняти їхню відбивну здатність рівною 0,7 (зверніть увагу на те, що, обчислюючи ефективну температуру, доводиться видобувати корінь четвертого степеня, а тому результат є малочутливим до вихідних даних, якщо відбивна здатність не зовсім близька до одиниці). Ефективна температура Венери виявляється рівною 290 К. Здавалося б, температура цілком придатна для життя. Але Венера — це не Місяць, вона має потужну атмосферу («знатну атмосферу», за висловом М. В. Ломоносова, який відкрив її 1761 р.). Складається ця атмосфера переважно з вуглекислого газу, який ефективно поглинає інфрачервоне випромінювання. Саме в цій частині спектра лежить максимум планківського випромінювання за розглядуваних температур (Т≥100 К). Атмосфера поглинає, а потім перевипромінює випромінювання поверхні планети частково в космос, а частково назад до поверхні. Унаслідок цього температура поверхні та нижньої атмосфери підвищується. Таке явище має назву парникового ефекту. На Венері це підвищення температури вельми значне. Температура поверхні Венери сягає 750 К, що підтверджено вимірами за допомогою радянських автоматичних станцій. Зрозуміло, що про жодні форми життя за таких умов не може бути й мови.

Заради справедливості треба зауважити, що тоді, коли М. Гумільов писав свого вірша, про все це ще не було відомо. Пробачимо поетові й те, що планету Венеру він назвав зорею.

12. Ця задача може видатися дуже простою. Усякий, хто бачив схід і захід Сонця, скаже, що воно в цей час має червоний колір. А зумовлюється це тією ж причиною, яка викликає почервоніння Місяця поблизу горизонту. Але слід згадати сказане наприкінці вступу до задач 10—14 про колір самосвітних тіл. Спробуємо з'ясувати, де лежить максимум прямого сонячного випромінювання, що пройшло крізь земну атмосферу. Це вже задача непроста. Розіб'ємо її розв'язання на чотири етапи. По-перше, з'ясуємо, якою була б висота земної атмосфери, якби вона була однорідною, тобто якби її густина не змінювалася з висотою. По-друге, знайдемо довжину шляху світлового променя в цій атмосфері для світила, яке спостерігається на горизонті. По-третє, з'ясуємо, як ослаблюється під час проходження атмосфери світло з різною довжиною хвилі. І, нарешті, знайдемо положення максимуму в спектрі сонячного випромінювання, яке пройшло крізь атмосферу.

1)     Висота однорідної атмосфери Н має бути такою, щоб вага її одиничного стовпа дорівнювала атмосферному тиску біля поверхні, тобто

Підставляючи сюди 

та

знайдемо, що Н=8 км.

2)     Довжина променя світла знаходиться з відповідного трикутника за теоремою Піфагора й дорівнює:

Тут ми знехтували відносно дуже малу величину Н².

 3)     Якщо світло проходить достатньо малу відстань ds, то його інтенсивність I зменшиться на малу величину dI, пропорційну пройденій відстані, тобто 

звідки

Інтегруючи, а потім потенціюючи останній вираз, мати­мемо:

Зауважимо, що отримана формула має назву закону Бу-гера.

4)     Тепер можна записати вираз для спектрального скла­ду сонячного випромінювання, що пройшло крізь земну атмосферу:

Лишилося знайти, за якого значення довжини хвилі А. функція І(λ) має максимум. Якщо підійти формально, то для цього слід знайти похідну функції та дорівняти її нулю. Але розв'язати одержане таким чином рівняння можна лише якимось числовим методом. Тому простіше обчислити таблицю значень функції І(λ). Почати обчислення можна зі значення λ=0,6 мкм, бо відшукуваний максимум лежить принаймні в червоній частині спектра, та обчислювати значення функції, збільшуючи значення довжини хвилі кожного разу на 0,1 мкм доти, доки значення функції не почнуть зменшуватися. Температура сонячної фотосфери дорівнює 5800 К, а коефіцієнт а (коефіцієнт ослаблення, або екстинкції) можна прийняти, як показують астрономічні спостереження, рівним 0,1 для довжини хвилі λ=0,6 мкм, а потім він зменшується обернено пропорційно четвертому степеню довжини хвилі світла. Результатом обчислень буде така таблиця (у відносних одиницях, без урахування постійного множника 2hc²): 

   Із цієї таблиці видно, що шуканий максимум лежить поблизу 1 мкм, тобто досить далеко в інфрачервоній частині спектра. Таким чином, відповідь на питання задачі буде такою: Сонце під час сходу та заходу є інфрачервоним, а те, що ми бачимо,— це червоний короткохвильовий «хвіст» прямого сонячного світла, яке пройшло крізь земну атмосферу.

 13. Енергія кожного фотона дорівнює

Тому й формулу Планка в цій задачі зручніше використати у вигляді залежності інтенсивності випромінювання від частоти:

Щоб знайти середню енергію фотонів, які випромінюються за даної температури, треба обчислити кількість цієї енергії в одиниці об'єму (густину енергії випромінювання) і поділити її на кількість фотонів в одиниці об'єму (їхню концентрацію). Формула Планка дає енергію, що випромінюється в одиничний тілесний кут. Це значить, що треба величину В_λ(Т) помножити на 4π — величину повного тілесного кута. Одиничну відстань фотони проходять за час, що дорівнює 1/с, де с — швидкість світла. Таким чином, повна густина енергії випромінювання на всіх частотах дорівнює:

Для того, щоб визначити концентрацію фотонів, слід спочатку знайти число фотонів із даною частотою ν , поділивши їхню повну енергію В_λ(Т) на енергію одного фотона hν , потім скласти всі ці числа (проінтегрувати за частотою). У результаті концентрація фотонів є такою:

Якщо в обох одержаних інтегралах замість В_λ(Т)  підставити його вираз і замінити в нихна х, то, ураховуючи, що

  

одержимо:

Поділивши першу рівність на другу, знайдемо, що середня енергія фотонів дорівнює: 

де коефіцієнт А дорівнює відношенню інтегралів у попередніх рівностях. Для спрощення цих інтегралів відкинемо в знаменниках підінтегральних виразів одиниці. За значень змінної х, значно більших від 1, це не спричиняє помітної похибки. Якщо х є близьким до 1, у самих підінтегральних виразах похибка буде відчутною, а у відношенні інтегралів вона значно зменшиться. Тепер 

Якщо подивитися в будь-який математичний довідник, у якому є таблиці інтегралів (а саме так зазвичай і роблять фізики та астрономи), побачимо, що

де n! (факторіал n) означає добуток усіх цілих чисел від 1 до п. Звідси випливає, що коефіцієнт А дорівнює 3 (точне ж його значення дорівнює 2,70). Зауважимо, що ці інтеграли не так вже важко знайти й без допомоги таблиць: для цього достатньо проінтегрувати перший із них за частинами тричі, а другий — двічі. 

 Обчислюючи тепер середню енергію фотонів сонячного випромінювання (T = 5800 К), знаходимо, що вона дорівнює:  

Це означає, що певна кількість сонячних фотонів має енергію в кілька електрон-вольт. Саме таку енергію мають електрони в атомах і молекулах, а значить, і енергії хімічних, а відтак і біохімічних процесів.

З цим і пов'язане зроблене в умові задачі твердження про Сонце як джерело життя на Землі.

 14. Для того щоб відповісти на поставлене питання, слід знайти середні концентрації нуклонів і фотонів у Всесвіті. Концентрація нуклонів знаходиться діленням середньої густини речовини (а це  ) на масу одного нуклона:

  Для визначення концентрації фотонів треба скористатися результатами попередньої задачі, з яких випливає, що ця концентрація, що дорівнює повній густині енергії випромінювання, поділеній на середню енергію одного фотона, становить:

Але яке ж значення температури треба взяти? Відомо, що весь Всесвіт рівномірно заповнений так званим реліктовим випромінюванням — фотонами, що залишилися від минулих епох еволюції Всесвіту. Що ж до випромінювання зір, то його густина спадає обернено пропорційно відстані від зорі, і тому його внесок в середню густину випромінювання нехтовно малий. Температура реліктового випромінювання зараз дуже невелика — усього 2,7 К. Це значення температури дає концентрацію фотонів, яка дорівнює приблизно 400 фотонам у кубічних сантиметрах. Таким чином, виявляється, що число фотонів у Всесвіті приблизно в сто мільйонів разів більше від числа нуклонів.

Результат може видатися несподіваним і дивним. Але дивним насправді є те, що у Всесвіті взагалі існує така відносно мала кількість нуклонів. Річ у тому, що, розширюючись, наш Всесвіт остигає. Коли в минулому температура Всесвіту була значно більшою від енергії спокою нуклонів (1,3 ГеВ), то нуклони й антинуклони перебували в стані термодинамічної рівноваги та існували в однакових кількостях. Коли ж температура стала меншою від енергії спокою нуклонів, то мала відбутися анігіляція нуклонів та антинуклонів. Чому ж певна кількість нуклонів збереглася? Це питання баріонної асиметрії Всесвіту. Одну з можливих відповідей на це питання дав академік А. Д. Сахаров. Виявляється, що швидкості реакцій перетворення пари «нуклон — антинуклон» на два гамма-кванти та оберненої реакції утворення такої пари з двох γ-квантів трохи різні. І цього «трохи» вистачило для того, щоб залишилася та кількість нуклонів, із яких складаємося і ми самі, і весь навколишній світ. Згідно із законом збереження електричного заряду, під час анігіляції електронів і позитронів залишилася й кількість електронів, що дорівнює кількості протонів.
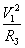